2. Методическая часть
Методическая часть
В первую очередь после изучения теоретической части необходимо разобраться, через какие методы и инструменты в Houdini может быть реализована рекурсия.
Основные подходы включают использование For-Each Loop, VEX и Solver. Каждый из них отличается степенью сложности, подходом и целью.

Краткое сравнение 3-х методов.
В рамках данной главы создана одна и та же сцена с применением всех трёх подходов. Это позволит наглядно показать различия в реализации каждого метода и закрепить понимание принципов их работы на практике. В качестве основы использована точка, которая проходит через заданный цикл. На каждом шаге она дублируется, а новая точка подвергается трансформации. Затем все точки объединяются, формируя непрерывный путь, который впоследствии преобразуется в кривую.
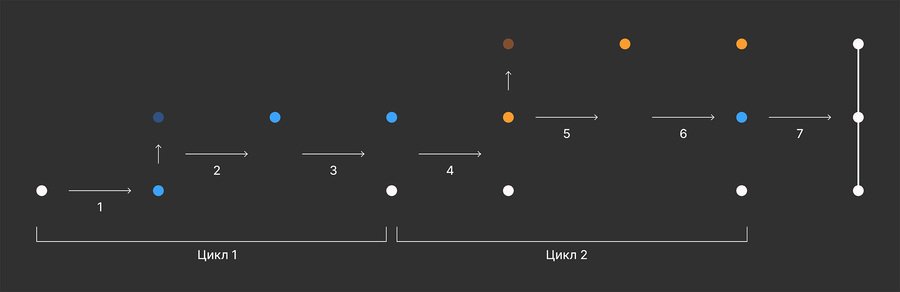
Принцип работы цикла в будущей сцене. 1 — копирование новой точки; 2 — трансформация новой точки; 3 — объединение новой и старой точек; 4-6 — аналогичны шагам 1-3; 7 — преобразование точек в кривую.
1. For-Each Loop
Принцип работы For-Each Loop
For-Each Loop — базовый инструмент, используемый для автоматизации повторяющихся операций над геометрией.
Его задача — взять определённый набор элементов (точки, примитивы, куски геометрии, числа и т. д.) и выполнить заданную цепочку нод столько раз, сколько требуется.
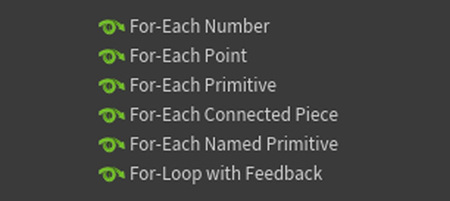
В TAB Menu (список нод, вызываемый Tab-ом) доступно шесть типов инструментов For-Each, отличающихся тем, как именно разбивается геометрия и какие данные проходят через цикл.
For-Each Number - цикл, повторяющийся фиксированное количество раз.
For-Each Point For-Each Primitive For-Each Connected Piece For-Each Named Primitive - циклы, имеющий похожий принцип: каждая итерация цикла проходит через отдельный элемент (точку, примитив, отдельный фрагмент или именованную часть).
For-Loop with Feedback - особый тип цикла, при котором результат каждой итерации передаётся в следующую.
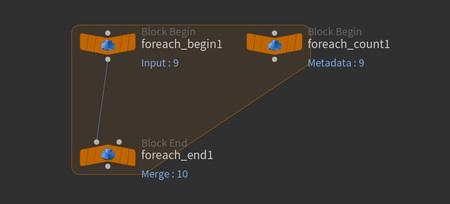
Инструмент For-Each Loop состоит из двух основных элементов:
Block Begin - входная точка цикла. - настройка метода цикла.
Block End - завершающая точка цикла. - сбор результатов всех итераций, настройка шагов, типа завершения цикла.
В некоторых случаях создаётся служебная нода Metadata - хранение данных о текущей итерации: номер шага, количество итераций, текущий элемент.
Принцип работы инструмента For-Each Loop. Куб состоит из 6 примитивов (полигонов), цикл выполняет 6 итераций.
Таким образом, принцип работы For-Each Loop заключается в том, что в Block Begin поступает геометрия, которая затем делится согласно выбранному типу (точки, примитивы, отдельные фрагменты или именованные части), после чего внутри цикла выполняется цепочка нод, применяемая к каждому элементу. Завершает процесс нодой Block End, где результаты всех итераций объединяются в итоговую геометрию.
Всё это позволяет гибко настраивать результат, добавлять вложенные циклы и быстро вносить необходимые изменения. Кроме того, структура представлена нодами, а не кодом, что визуально и технически упрощает работу.
Практическая реализация For-Each Loop
Интерфейс Houdini. 1 — вьюпорт (viewport); 2 — панель параметров; 3 — панель нод.
В новом проекте Houdini в панели нод создаётся нода «Geometry» (пустая нода геометрии). После двойного нажатия ЛКМ по ней открывается её внутренняя структура — уровень SOP.
SOP (Surface Operators) — это уровень работы в Houdini, предназначенный для выполнения операций с геометрией.
Создание ноды Geometry в панели нод.
В первую очередь, необходимо создать точку, с которой начинается построение системы. Для этого добавляется нода «Add».
Нода «Add» Создание точек и их соединение в примитивы по заданными условиям.
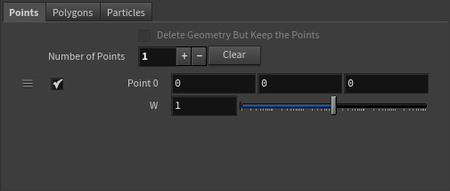
В Parameters (окно настройки ноды) во вкладке Points нажимается +, в результате чего создаётся точка. Ниже отображена информация о ней: её номер и координаты. В данном случае, настройки остаются по умолчанию.
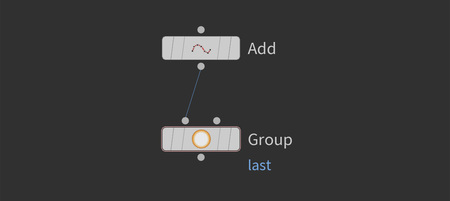
Затем добавляется нода «Group». Это определяет группу, на которую применяется трансформация в последующем цикле.

Нода «Group» Генерация группы из точек, примитивов, эджей или вершин по заданным условиям.
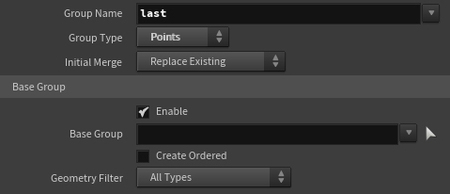
Группе присваивается имя last в Group Name (название можно изменить при необходимости). Параметр Group Type — Points, поскольку работа ведётся с точками. Остальные параметры остаются без изменений.
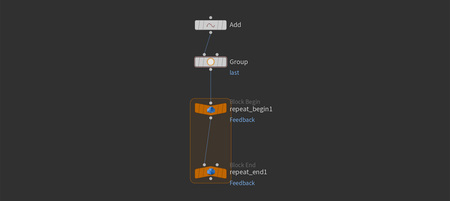
Далее создаётся нода For-Loop with Feedback. Используется именно вариант с feedback, так как он позволяет на каждом шаге цикла использовать результат предыдущей итерации, что необходимо для постепенного наращивания геометрии.
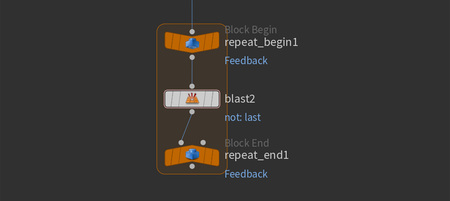
Внутри цикла добавляется нода «Blast», которая удаляет все точки, кроме последней, к которой применяется трансформация (то есть к точке в группе last).
Нода «Blast» Удаление примитивов, эджей, точек.
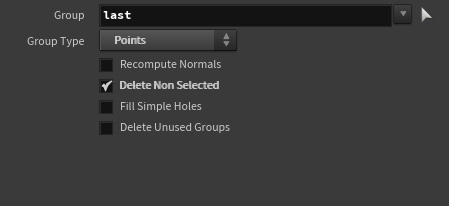
Для того, чтобы оставить только последнюю точку в Group назначается группа last, Group Type — Points, и активируется опция Delete Non-Selected.
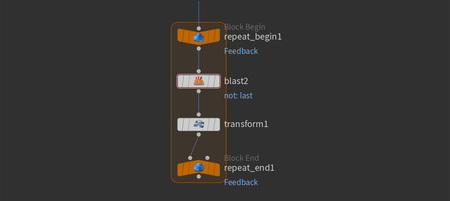
Следом добавляется нода «Transform», с помощью которой последняя точка перемещается в пространстве.

Нода «Transform» Трансформация геометрии (перемещение, вращение, масштаб и центровку) в 3D-пространстве.
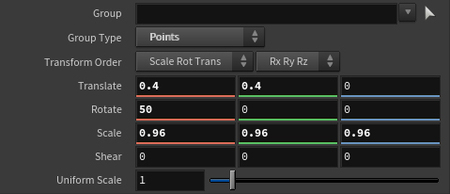
Параметры трансформации могут быть заданы произвольно, однако для воспроизводимости эксперимента они остаются постоянными.
Translate — позиция; Rotate — поворот; Scale — размер.
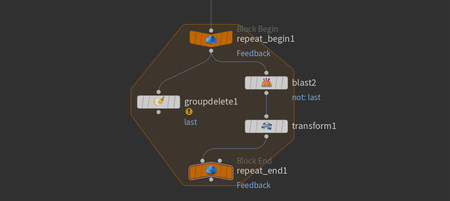
Операции с новой точкой закончены. Теперь от начальной ноды цикла добавляется нода «Group Delete».

Нода «Group Delete» Удаление группы из точек, примитивов, эджей или вершин по заданным условиям.
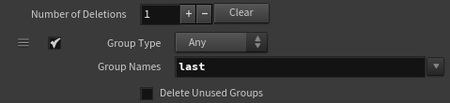
В параметрах в Group Names выбирается группа last. Это необходимо для удаления группы с уже обработанных точек, чтобы они не участвовали в последующих трансформациях.
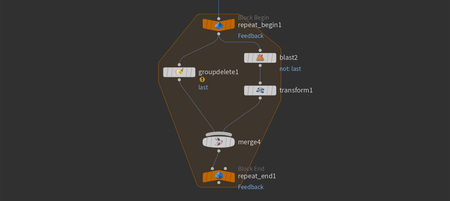
После этого создаётся нода «Merge», и всё это подключается к концу цикла.

Нода «Merge» Объединение геометрии из нескольких входов.
Таким образом, точки, созданные на предыдущих шагах, соединяются с новой, трансформированной, и вся операция выполняется внутри цикла.
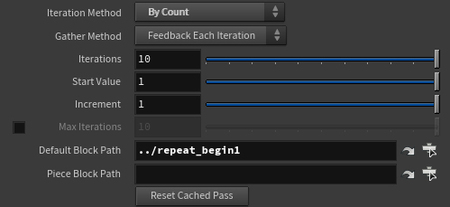
В настройках ноды «Block End» можно задать количество шагов (Iterations), определяющее длину создаваемого пути.
Влияние параметра Iterations на цикл.
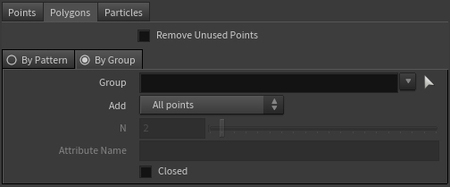
После завершения цикла точки можно объединить в кривую. Для этого используется нода «Add»: во вкладке Polygons выбирается режим By Group, в результате чего последовательность точек превращается в кривую.
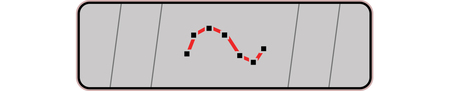
Работа ноды «Add»: соединение последовательности точек в кривую.
Готовая сцена.
2.2. VEX
Принцип работы VEX
VEX (Vector Expression Language) — это встроенный язык программирования в Houdini.
VEX позволяет описывать поведение объектов не через набор нод, а напрямую через код, что делает его одним из наиболее гибких и точных инструментов моделирования.
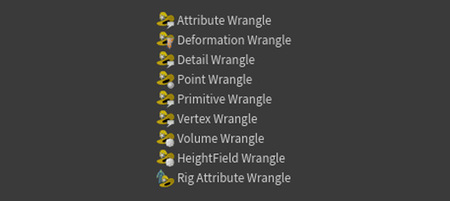
В TAB Menu доступно несколько вариаций инструментов Wrangle. Они различаются уровнем геометрии, на котором выполняется код: над точками, примитивами и так далее. Несмотря на это, принцип работы у них один — выполнение VEX-кода над входящей геометрией.
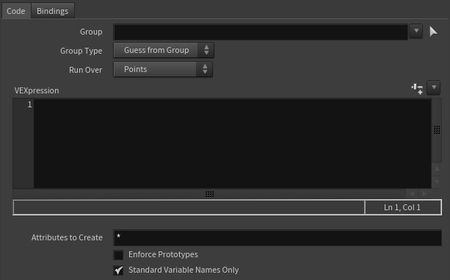
Во всех типах Wrangle параметры устроены одинаково: поле выбора группы, настройка уровня геометрии и, самое главное, — поле для написания VEX-выражений.
Основным инструментом в рамках данного проекта является нода «Attribute Wrangle».

Нода «Attribute Wrangle» Выполнение VEX-кода для изменения атрибутов и их значений.
Атрибут — это единица данных, которая хранится на различных уровнях геометрии.

При нажатии средней кнопкой мыши на ноду можно увидеть все существующие виды атрибутов (при их наличии): - point attributes — на точках; - primitive attributes — на примитивах; - vertex attributes — на вершинах; - detail attributes — на уровне объекта целиком.
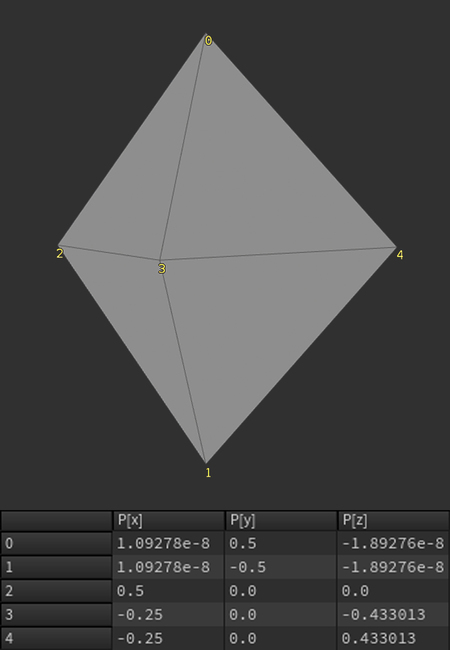
Самым наглядным атрибутом является атрибут точек P, поскольку именно он задаёт положение геометрии в пространстве.
На схеме видно, что у каждой точки (0–4) есть собственный атрибут P (в данном случае, он состоит из трёх компонентов P[x], P[y], P[z], соответствующих осям 3D-пространства), который напрямую определяет форму объекта.
Атрибут Cd (цвет) с рандомными значениями на разных уровнях геометрии: detail, primitive, point и vertex соответственно. Всё это влияет на итоговый визуальный результат.
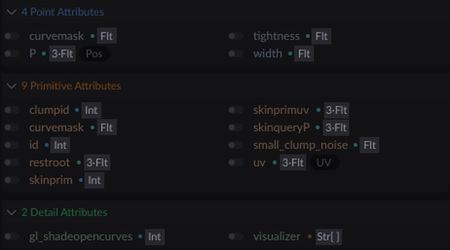
Атрибуты могут содержать данные разных типов. Самые базовые из них: - float — число с плавающей точкой (например, 10.5; -0.76); - integer — целое число (например, 13, -5, 0); - vector — три числа (иногда записаны как 3flt) - string — строка из символов.
Например, атрибут P — векторный, так как совмещает в себе три значения: P[x], P[y], P[z].
В отличие от нодовой структуры, где рекурсия реализуется через построение цепочек и циклических блоков, в VEX ключевым механизмом становится программный цикл, выполняющийся в рамках одной ноды.
Для повторения последовательности операций используется конструкция for:
for (int i = 0; i < chi («iterations»); i++) { … }
- for (…) — цикл, выполняющий блок кода в {}; - int i=0 — создание счётчика, начинающегося с нуля; - i<chi («iterations») — условие продолжения: функция chi () считывает integer-параметр iterations, поэтому цикл выполняется указанное количество раз; - i++ — увеличение счётчика на 1 каждую итерацию.
Таким образом, логика, которая в нодовой структуре требовала множества нод, в VEX превращается в компактный алгоритм, выполняющийся последовательно внутри одного блока кода.
Такой подход обеспечивает гибкость, максимальную точность и структурную простоту, однако требует знания синтаксиса и понимания принципов работы атрибутов.
Практическая реализация VEX
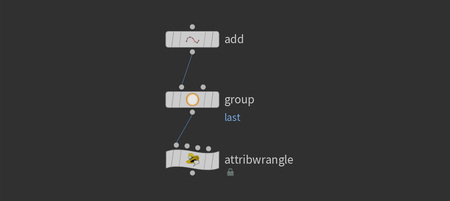
На первом этапе часть Add-Group копируется из предыдущего сетапа. После этого подключается нода Attribute Wrangle, в которой пишется VEX-код.
Код внутри Attribute Wrangle выступает альтернативой части For-Each Loop, однако его логика несколько иная, поэтому необходимо подробно разобрать каждую строчку.
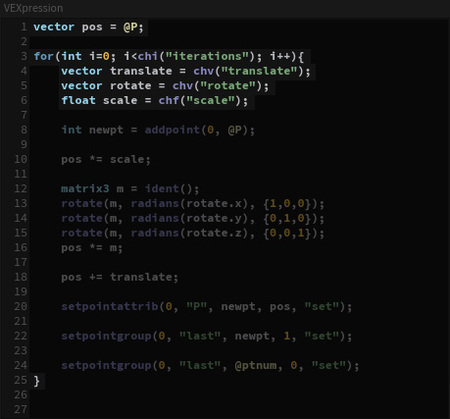
vector pos = @P; - создание локальной переменной pos типа vector и сохранение в нее текущей позиции точки.
for (int i=0; i<chi («iterations»); i++){…}; - создание цикла.
vector translate = chv («translate»); vector rotate = chv («rotate»); float scale = chf («scale»); - создание 3-х параметров, эквивалентных настройкам transform ноды. - chv и chf позволяют создать управляемые параметры типа vector и float соответственно с заданными в скобках названиями.
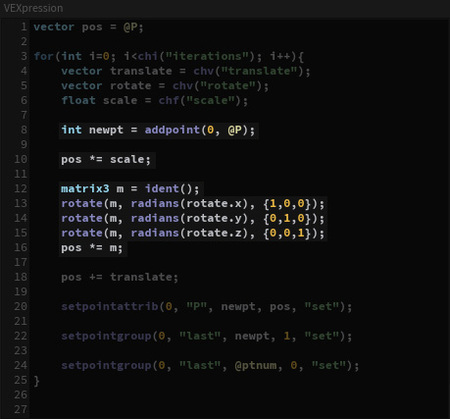
int newpt = addpoint (0, @P); - addpoint (geohandle, position) — создание новой точки с заданной позицией. - сохранение индекса созданной точки
pos *= scale; - применение scale на позицию (уменьшение или увеличение) относительно начала координат.
matrix3 m = ident (); rotate (m, radians (rotate.x), {1,0,0}); rotate (m, radians (rotate.y), {0,1,0}); rotate (m, radians (rotate.z), {0,0,1}); pos *= m; - блок, отвечающий за поворот точки - matrix3 m = ident (); — создание 3×3 матрицу. - rotate (m, angle, axis) — поворот вокруг axis (вектор оси), добавление вращения в матрицу m; angle в радианах. - radians (rotate.x) — перевод градусов в радианы. - pos *= m; — умножение pos (позицию) на матрицу m, т. е. поворачивает точку.
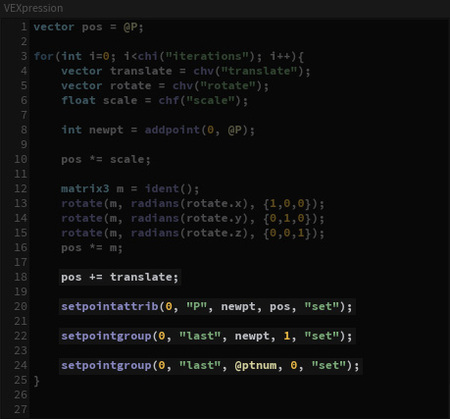
pos += translate; - добавление вектора смещения translate к позиции pos
setpointattrib (0, «P», newpt, pos, «set»); - setpointattrib (geohandle, attribname, pointnum, value, mode) — запись значения value атрибута attribname на конкретную точку pointnum. - в данном случае новая позиция pos записывается в атрибут P новой точки newpt (то есть, применяется трансформация на новой точке) - set — режим записи (заменяет значение).
setpointgroup (0, «last», newpt, 1, «set»); setpointgroup (0, «last», @ptnum, 0, «set»); - setpointgroup (geohandle, groupname, pointnum, value, mode) — добавление/удаление точки pointnum в/из группы groupname. value = 1 — добавление, value = 0 — удаление. - setpointgroup (…, newpt, 1, «set») — добавление созданной точки в группу last. - setpointgroup (…, @ptnum, 0, «set») — удаление исходной точки из группы last (в результате в группе остаётся только последняя).
Нажатием на Creates spare parameters в интерфейсе ноды появляются дополнительные параметры: Translate, Rotate, Scale и Iterations. Их значения дублируют настройки из прошлого примера для создания одинакового результата.
Включение дополнительных параметров.
Изменение добавленных параметров.
После выполнения цикла через VEX добавляется завершающая нода «Add» из прошлого сетапа. Она соединяет вычисленные точки в кривую.
Готовая сцена.
2.3. Solver
Описание принципа Solver
Solver — инструмент Houdini, позволяющий выполнять нодовую сеть не однократно, а пошагово: результат каждой итерации автоматически передаётся в следующую (на основе кадров).
В основе инструмента лежит одноимённая нода «Solver».
Нода «Solver» Выполнение определенной нодовой сети на каждом кадре, где результат предыдущего кадра используется как исходные данные.

После создания ноды в SOP необходимо перейти в ее внутреннюю структуру двойным нажатием ЛКМ. Внутри изначально представлено несколько нод: - Prev_Frame — результат предыдущего кадра; - Output — точка выхода. - Input 1, Input 2, Input 3, Input 4 — входы для исходной геометрии; данные с них доступны на каждом шаге цикла.
Внутри Solver находится аналогичный уровень геометрии, что и SOP, поэтому в нем можно строить любую нодовую логику.
Принцип работы Solver.
В приведённом примере показан принцип работы Solver. На первом кадре куб объединяется со сферой и проходит трансформацию, после чего результат отправляется на выход. На следующем кадре уже изменённая геометрия снова объединяется со сферой и повторяет те же операции. Процесс повторяется каждый кадр, исходная геометрия из входов остаётся неизменной, а итоговая постепенно усложняется.
Таким образом, Solver позволяет в рамках одной ноды автоматически накапливать изменения геометрии от кадра к кадру и выстраивать сложные процессы на основе нескольких потоков данных. Однако симуляционная природа усложняет отладку, а необходимость работать с разными уровнями геометрии на каждом шаге делает инструмент более трудоёмким.
Практическая реализация Solver
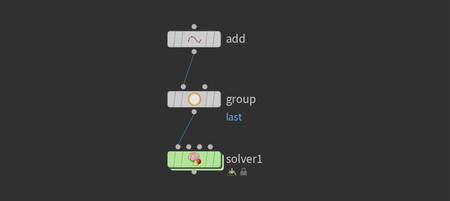
Как и в прошлом примере, часть Add-Group переносится из первого сетапа. После чего подключается нода «Solver», внутрь которой необходимо зайти для настройки операций цикла.
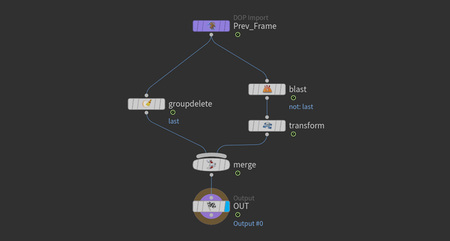
Внутри «Solver» вставляются ноды из первого сетапа (groupdelete, blast, transform, merge) и подключаются между Prev_Frame и Out без изменения настроек.
После этого на уровне SOP при запуске проигрывания таймлайна начинается цикл итераций.
Проигрывание цикла.
По примеру прошлых сетапов, всё заканчивается нодой «Add» с заданными настройками.
Готовая сцена.
Houdini [Электронный ресурс] // SideFX. — URL: https://www.sidefx.com/docs/houdini/index.html (дата обращения: 21.11.2025).



